|
|
|
|
Schauen Sie doch einmal in einen Karton Megaperls oder in eine Packung Feinfrosterbsen! Sie sehen eine Menge von Kugeln, die zwar unordentlich angeordnet sind, aber ziemlich dicht liegen. Wären die Kugeln aus hartem Metall, könnte man sie noch schütteln und pressen. Auf jeden Fall erhielte man aber ein zufälliges System dicht gepackter Kugeln. Ähnliche Strukturen bilden die Atome in sogenannten metallischen Gläsern, die Poren in Porenbeton (ja, wirklich die Poren) oder die Metallteilchen in Sinterwerkstoffen.
Mathematiker, Physiker und Werkstoffwissenschaftler haben die Vorstellung von einem unendlich ausgedehnten System von zufällig angeordneten Kugeln, einer dichten zufälligen Kugelpackung. Eine mathematische Beschreibung und die Herleitung von Formeln gelang für diese Struktur bisher nicht. Das mag verwundern, weil es doch hierbei um ein rein geometrisches Problem geht.
In den fünfziger Jahren hat, wohl aus Verzweiflung über die Mathematik, der berühmte Physiker J.D. Bernal Metallkugeln in ein großes Gefäß gefüllt, sie lange geschüttelt und schließlich gepreßt. Danach hat er Wachs in das Gefäß gegossen, um die Positionen der Kugeln zu fixieren. Dann wurden die Kugeln nacheinander dem Gefäß entnommen und die Koordinaten der Kugelmittelpunkte vermessen. Schließlich hat Bernal das System der (x,y,z)-Koordinaten statistisch analysiert.
Durch dieses und weitere Experimente weiß man vieles über
die Anordnung der Kugeln: z.B. wurde die zufällige Verteilung der
Anzahl der Nachbarn einer beliebig herausgegriffenen Kugel recht gut untersucht
und man hat auch festgestellt, daß der Volumenanteil der Kugeln,
d.h. derjenige Anteil des Raumes, der von den Kugeln eingenommen wird,
etwa (oder wie manche vermuten, ) beträgt.
|
|
Wegen der großen praktischen Bedeutung von zufälligen Kugelpackungen können die Physiker und Angewandten Mathematiker nun nicht darauf warten, eines Tages von der Theorie her vielleicht doch noch eine Lösung zu erhalten. Man begann daher, das Problem durch Simulation zu erforschen. Das heißt, man erzeugt mit Hilfe von Zufallszahlen im Computer numerische Dateien für zufällige Systeme von dicht gepackten Kugeln.
In den siebziger Jahren hat man zunächst den der Schwerkraft folgenden
Prozeß der Packung von Kugeln in einem Behälter nachgebildet.
Wenn also schon n Kugeln im Behälter sind, fällt die (n+1)-te
Kugel auf den Haufen der Kugeln. Sie rollt dann abwärts und bleibt
irgendwo, dem Zufall folgend, liegen. Bei einfachen Programmen hat man
die Kugel drei- oder fünfmal rollen lassen und sie dann liegen lassen,
auch wenn ihr Standort physikalisch unsinnig war, z.B. über einem
Loch schwebend. Man erreichte auf diese Art und Weise Packungsdichten von
etwa 60 %. Je höher die erreichte Packungsdichte war, desto stolzer
war der Programmierer.
|
|
Dr. U. Jansen von unserem Institut für Stochastik simuliert Kugelpackungen anders. Er plaziert eine Kugel im Koordinatenursprung und lagert dann sukzessive von außen weitere Kugeln an. So entsteht ein Ball von Kugeln, der allmählich wächst. Die Abbildungen 1 und 3 zeigen solche Systeme von Kugeln, in den zugehörigen Abbildungen 2 und 4 sieht man deren ebene Schnitte.
Dr. Jansen erreicht so Packungsdichten von 64 - 65 %. Dieser etwas zu große Wert hängt mit dem Start der Simulation zusammen. Das genügt für sein Forschungsthema, in dem er für das Keramikinstitut Meißen Systeme von Keramikpartikeln studiert. Dabei sind seine Kugeln nicht gleich groß, sondern haben variable Radien. Ziel der Untersuchungen war die Herstellung von Feinkeramik mittels der Preßtechnologie. Die Kugeln entsprechen Porzellanrohmassenteilchen im Granulat.
Ich habe seit längerer Zeit sogenannte Gibbsprozesse studiert. Das sind zufällige Systeme von Kugeln im Raum, zwischen denen Kräfte wirken, die dafür sorgen, daß sich die Kugeln, je nachdem, anziehen oder abstoßen. Benannt sind sie nach dem amerikanischen Physiker J. Gibbs. Bei harten Kugeln sind die Kräfte besonders einfach: totale Abstoßung, wenn die Kugeln in Kontakt kommen, und gar keine Beeinflussung bei größeren Abständen.
|
er hat seine Gesetzmäßigkeiten." Novalis (Frieder von Hardenberg) studierte 1797/98 an der Bergakademie Freiberg |
Das zugehörige Modell heißt "Poisson-Hard-Core-Prozeß" (PHCP). Dessen Packungsdichte wird durch einen Parameter a gesteuert, der chemische Aktivität genannt wird. Mein Assistent Herr St. Berndt erzeugte nun nach einem bewährten Rezept im Computer Kugelsysteme nach dem PHCP für verschiedene Werte von a . Wie erwartet ergab sich, daß die Packungsdichte mit abnehmendem a anstieg. Es schien so, als würde sie für sehr negative Werte von a (also für "minus Unendlich") den Wert 40 % erreichen.
In dem internationalen Standardwerk "Stochastic Geometry and its Applications" (erschienen 1995 bei Wiley), das ich zusammen mit den Herren Professoren Mecke aus Jena und Kendall aus Coventry schrieb, ist ein Diagramm zu sehen, das diesen Zusammenhang zwischen Packungsdichte und a zeigt. Zum Glück wurde dort nicht behauptet, daß 40 % der größtmögliche Wert für die Kugeldichte sei.
Im letzten Winter kamen mir Zweifel wegen des Zahlenwerts 40%. Ich fragte einen der führendenen Spezialisten der Welt für unendliche Gibbsprozesse, den Japaner Professor S. Mase , per e-mail nach seiner Meinung. Man muß dazu bemerken, daß ich bereits früher viele europäische Kollegen befragt habe, aber diese hatten mich nicht so richtig verstanden, weil sie nur endliche Gibbsprozesse untersuchen.
Professor Mase begriff recht schnell, um was es mir hierbei ging, und dachte über das Problem nach. Im Februar diesen Jahres war in Oberwolfach im Schwarzwald eine Tagung über Punktprozesse. Dort konnten Professor Mase und ich endlich persönlich miteinander diskutieren. Professor Mase setzte sich nachts hin und fand einen Beweis für die Aussage, daß die vom PHCP maximal erreichbare Packungsdichte sehr hoch ist, nämlich etwa 74 %. Das ist der Wert, der erreicht wird, wenn man gleich große Kugeln gitterförmig so packt, daß die Packungsdichte maximal wird (vgl. auch den Beitrag zum Keplerschen Kugelproblem ). Das Problem wurde beim Mittagessen in Oberwolfach mit dem dänischen Professor J. Moller diskutiert, der mit Professor Mase über Einzelheiten des Beweises sprach und einen Weg zu haben glaubte, um PHCP bei sehr kleinen Werten von a zu simulieren. Der Fehlschlag der Simulation von Herrn Berndt hat ihn nicht überrascht, dessen Methode funktioniert offensichtlich nur bei geringen Packungsdichten.
Alle drei und ein Doktorand von Professor Moller wollen nun die Beweise ordnen, über die Simulation nachdenken und schließlich simulierte Kugelsysteme statistisch analysieren, etwa so, wie es einst der Physiker Bernal machte, jetzt aber mit simulierten Systemen und nicht mit selbst gepackten. Eine spannende Frage ist, was passiert, wenn man die Parameter des PHCP so wählt, daß sich eine Packungsdichte von 63 % ergibt. Kommt dann vielleicht eine dichteste zufällige Kugelpackung heraus?
Zufällige Kugelsysteme begegnen uns noch in anderen
Situationen. Die Löcher in Schweizer Käse sind auch oft kugelförmig,
aber sie durchdringen einander. Man kann sich vorstellen, daß im
Käsekörper zufällige Punkte verteilt sind, die Mittelpunkte
von Kugeln mit zufälligen Radien darstellen. Die Bilder 5, 6 und 7
zeigen solche Systeme, genauer ebene Schnitte durch Systeme von einander
überlappenden Kugeln mit zufälligen Mittelpunkten.

Bild 5: Boolesches Modell |
Ähnliche Systeme treten ebenfalls sehr häufig auf, z.B. in den Werkstoffwissenschaften, in der Physik und in der Ökologie. Auch eine Schnitte vom "richtigem" Brot zeigt ein System von Poren, die offensichtlich zufällig sind und sich durchdringen. Hierfür haben die Mathematiker ein Modell entwickelt, das Boolesches Modell heißt. Hier stand der englische Logiker G. Boole für den Namen Pate. Im Gegensatz zur zufälligen Kugelpackung gibt es für das Boolesche Modell eine Vielzahl von Formeln. Dafür ist aber die Statistik schwieriger.
Es ist relativ leicht, die Anzahl von sich nicht überschneidenden
Kugeln in einem bestimmten Bereich des Raumes zu bestimmen. Wenn sich aber
die Kugeln bzw. deren ebene Projektionen überlappen, dann gibt es
Probleme. Man versuche beispielsweise einmal, die Anzahl der Kreise in
Bild 5 oder Bild 7 zu bestimmen. Es wird hier Zweifel geben im Zusammenhang
mit den Bereichen, in denen die Kreise sehr dicht liegen, wo man nicht
sicher ist, ob nicht vielleicht einige Kreise total überdeckt worden
sind. Noch schwieriger wird es, wenn an die Stelle von Kugeln andere, kompliziertere
Figuren treten, wie z.B. bei den Brotporen.
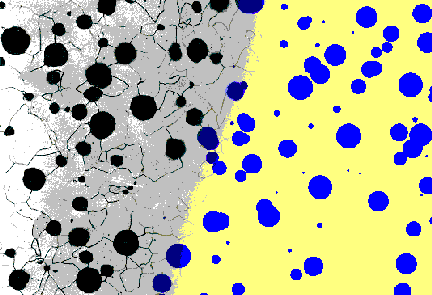
Bild 6: Graphitkugeln in Gußeisen (links)
|
Es gibt aber Verfahren, um die Dichte der Kugeln (die
mittlere Anzahl je Volumeneinheit) statistisch zu ermitteln. Der Trick
dabei besteht darin, sich nicht mehr auf die Mittelpunkte (wie den Erdmittelpunkt)
zu konzentrieren, sondern auf die unteren Tangentenpunkte (wie den Südpol)
der Teilchen. Die sind leichter zu ermitteln, wobei es bei "vernünftigen"
Teilchen genauso viele Mittelpunkte wie untere Tangentenpunkte gibt. Man
kann sich nun überlegen, daß der Anteil der unteren Tangentenpunkte,
die von anderen Teilchen überdeckt werden, gleich dem Volumenanteil
des Booleschen Modells ist. Damit erhält man für die Punktdichte
p und die Dichte der Tangentenpunkte t die Formel t =
p (1 - V) wobei V den Volumenanteil bezeichnet. Damit kann man
die Punktdichte statistisch ermitteln, indem man Tangentenpunkte zählt
und den Volumenanteil bestimmt.
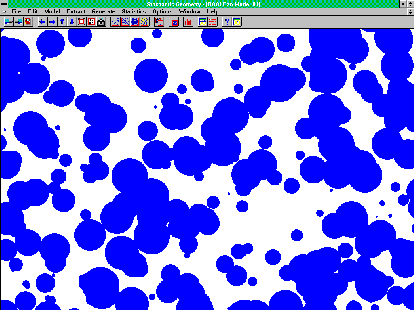
Bild 7: Ein weiteres Boolesches Modell |
Klar ist, daß dabei die Genauigkeit von der Größe
des Untersuchungsgebiets abhängt, in dem man die Tangentenpunkte zählt
und den Volumenanteil ermittelt. Wenn man nun den Einfluß dieser
Größe studieren will, was für die Planung von Messungen
praktisch sehr wichtig ist, dann sind ziemlich schwierige mathematische
Rechnungen erforderlich. Man wendet Verfahren aus der stochastischen
Geometrie und räumlichen Statistik an.
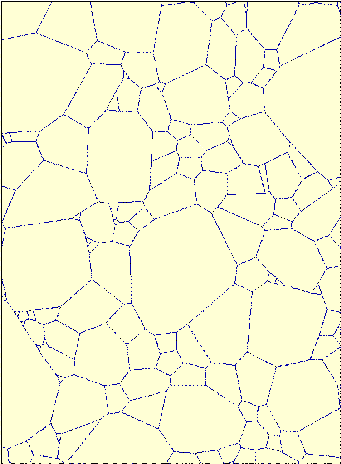
Bild 8: Zufällige Voronoi-Mosaike |
Freiberg ist in Deutschland das Zentrum für diese
Zweige der Stochastik. So ist es auch natürlich, daß gerade
in Freiberg das Graduiertenkolleg "Räumliche Statistik" arbeitet.
Hier sind zur Zeit 10 Doktoranden tätig, die gemeinsam theoretische
und praktische Fragen der Analyse räumlicher Daten studieren. Dabei
spielen auch Fragen der
Geostatistik und der Informationsübertragung
eine bedeutende Rolle. (Weitere Informationen dazu finden sich in den
Notizen aus dem Fakultätsleben im Beitrag: Graduiertenkolleg
"Räumliche Statistik" .)
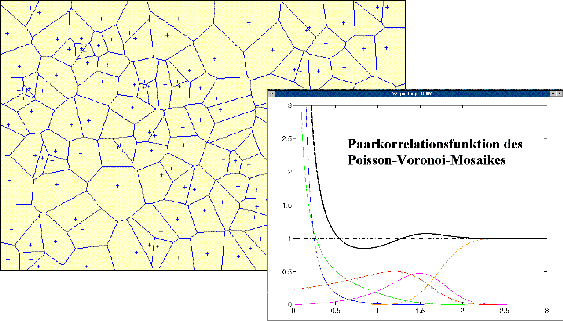
Bild 9: Stochastische Geometrie und Räumliche Statistik |
Mosaike sind Modelle der Stochastischen Geometrie, die
in Freiberg besonders intensiv untersucht werden. Viele wichtige Materialparameter
(z.B. Festigkeit, thermische Belastbarkeit, Homogenität, u.a.) stehen
in enger Beziehung zu der Gestalt der Zellen. Das linke Bild zeigt einen
Anschliff eines Materials. Ziel der Modellierung ist eine theoretische
(d.h. mathematische) Darstellung des Gefüges. Dazu lassen sich beispielsweise
die sogenannten Voronoi- Mosaike verwenden. Für diesen Typ von Mosaiken
können beschreibende Parameter (z.B. mittlere Eckenzahl, mittlere
Zellfläche, mittlere Kantenlänge, u.a.) explizit berechnet werden.
|
|
Die Freiberger räumlichen Statistiker arbeiten eng
mit verschiedenen Industriebetrieben zusammen, die Stoffe wie Halbleiter,
Stahlgußteile und Porzellan herstellen. Daher stehen Praktikumsplätze
und angewandte Diplomarbeitsthemen reichlich zur Verfügung.
Prof. Dr. Dietrich Stoyan
Institut für Stochastik
Fakultät für Mathematik und Informatik
TU Bergakademie Freiberg

|

|

Notzien
aus dem Fakultätsleben:
|